FFT 推导过程

所有考试总算考完了，于是我被 L^AJ_i 学校坑去生产线 QAQ

趁着脑袋还记得先马一下（距离遗忘 DSP 所有内容还有 30min

计算过程

已知\(X[m]=\sum_{k=0}^{N-1}x[k]W_{N}^{km},m=0,1,...N-1\)

那么

\[\begin{align*} X[m] &= \sum_{k=0}^{N-1}[k==2r]x[k]W_{N}^{km}+\sum_{k=0}^{N-1}[k==2r+1]x[k]W_{N}^{km} \\ &= \sum_{r=0}^{N/2-1}x[2r]W_{N}^{2rm}+\sum_{r=0}^{N/2-1}x[2r+1]W_{N}^{(2r+1)m} \\ &= \sum_{r=0}^{N/2-1}x[2r]W_{N}^{2rm}+W_{N}^{m}\sum_{r=0}^{N/2-1}x[2r+1]W_{N}^{2rm} \\ &= \sum_{r=0}^{N/2-1}x_1[r]W_{N}^{2rm}+W_{N}^{m}\sum_{r=0}^{N/2-1}x_2[r]W_{N}^{2rm} \end{align*}\]

由可约，

\[\begin{align*} X[m] &= \sum_{r=0}^{N/2-1}x_1[r]W_{N/2}^{rm}+W_{N}^{m}\sum_{r=0}^{N/2-1}x_2[r]W_{N/2}^{rm} \\ &= X_1[m]+X_2[m] \\ \end{align*}\]

由周期，

\[X_1[m+N/2]=X_1[m]\] \[X_2[m+N/2]=X_2[m]\]

由对称，

\[W_{N}^{m+N/2}=-W_{N}^{m}\]

可得到另一边

\[X[m+N/2]=X_1[m+N/2]+W_{N}^{m+N/2}X_2[m+N/2]=X_1[m]-W_{N}^{m}X_2[m]\]

对比一下

\[\begin{align*} X[m] &= X_1[m]+W_{N}^{m}X_2[m] \\ X[m+N/2] &= X_1[m]-W_{N}^{m}X_2[m] \end{align*}\]

可以得出复杂度 \(T(n) = 2T(n/2)+O(n)\)

FFT 流程图要点

1. 过程我觉得按照自底向上的写法比较好
2. 原输入顺序是通过二进制的翻转 (不是反) 来确认的

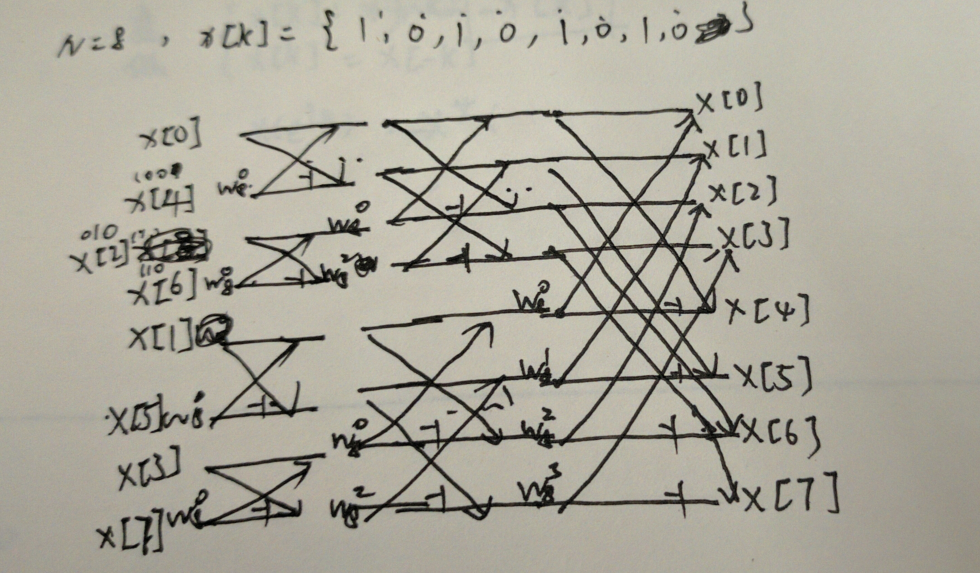
本来考试前画了一张挺漂亮的图但找不到了..

换了一张灵魂作图